贵州省高考数学2017_贵州省高考数学2023

1.2017高中数学面积体积公式

2.2017年各省高考总分分别是多少

3.贵州历年高考分数线

4.2017年全国一卷数学高考题，如图，答案最后为什么写m＞负一？

贵州高考科目包括文化课和综合素质评价两个部分。

其中，文化课包括语文、数学、外语、物理和化学等5门科目；综合素质评价则包括思想品德、艺术素养、体育素质和实践能力等4个方面。

一、文化课科目

1、语文：语文是文化课中的必修科目，主要考察学生的语言文字表达、阅读理解和写作能力等；数学：数学也是文化课中的必修科目，主要考察学生的数学知识和解题能力等。

2、外语：外语包括英语和其他小语种，是文化课中的选修科目之一，主要考察学生的听、说、读、写能力。

3、物理：物理是文化课中的必修科目之一，主要考察学生的物理知识和实验能力等；化学：化学也是文化课中的必修科目之一，主要考察学生的化学知识和实验能力等。

二、综合素质评价科目

1、思想品德：思想品德是综合素质评价中的重要评价内容，旨在考察学生的思想道德素质、法律意识和公民意识等。

2、艺术素养：艺术素养也是综合素质评价中的重要评价内容，旨在考察学生的音乐、舞蹈、美术和戏剧等方面的基本素养。

3、体育素质：体育素质包括体力、技能和心理等方面的测评内容，旨在考察学生的运动素质和健康状况等。

4、实践能力：实践能力是综合素质评价中的另一个重要评价内容，旨在考察学生的实践能力和综合素质等。实践能力评价包括社会实践、科技创新、文化艺术和体育竞技等方面。

拓展知识——贵州省高考

1、自2017年起，贵州省高考开始实行“综合素质评价+普通高考”模式，将学生的考试成绩与综合素质评价相结合，作为高校录取的重要依据。

2、这种改革旨在促进教育的全面发展，重视学生素质的培养和实践能力的提高。同时也提升了高校对学生的素质要求，推动高等教育向质量和创新驱动转变。

3、在日益激烈的就业竞争中，学生应该注重素质拓展和实践能力的提高，既要有过硬的文化素养，又要有综合素质的全面发展，才能更好地适应未来的职业要求。

2017高中数学面积体积公式

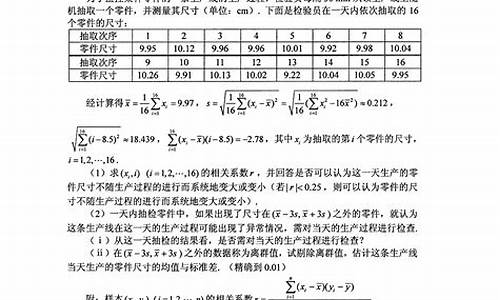
作为一个8年前参加高考的老人来说，这个题目的话，设三角形ABC边长为X，体积为Y，然后取X范围为0~5根号3。然后你等边三角形ABC的话，你面积可以算出来，差不多是根号3/4的X?。然后高度的话，OF=5cm，然后减去O到AB的垂线距离，多少我懒得算了，反正不难。接下来三棱锥的体积公式算出来，然后根据x的范围，求出最大值。我记得好像要靠导数的，忘了，嘿嘿。

2017年各省高考总分分别是多少

几何题复习最重要的就是要掌握好相应的高中数学面积以及体积公式，这样才能避免在高中数学几何题中丢分。接下来我为你整理了高中数学面积体积公式，一起来记一记吧。

高中数学面积体积公式1-5

　1、圆柱体:

　表面积:2?Rr+2?Rh

　体积:?R2h (R为圆柱体上下底圆半径,h为圆柱体高)

　2、圆锥体:

　表面积:?R2+?R[(h2+R2)的平方根]

　体积: ?R2h/3 (r为圆锥体低圆半径,h为其高,

　3、正方体

　a-边长， S=6a2 ，

　V=a3

　4、长方体

　a-长 ,b-宽 ,c-高 S=2(ab+ac+bc) V=abc

　5、棱柱 、 S-底面积 h-高

　V=Sh

高中数学面积体积公式6-10

　6、棱锥

　S-底面积 h-高

　V=Sh/3

　7、棱台

　S1和S2-上、下底面积 h-高

　V=h[S1+S2+(S1S2)^1/2]/3

　8、拟柱体

　S1-上底面积 ，S2-下底面积 ，S0-中截面积 h-高，

　V=h(S1+S2+4S0)/6

　9、圆柱

　r-底半径 ，h-高 ，C?底面周长 S底?底面积 ，S侧?侧面积 ，S表?表面积

　C=2?r

　S底=?r2，

　S侧=Ch ，

　S表=Ch+2S底 ，

　V=S底h=?r2h

　10、空心圆柱

　R-外圆半径 ，r-内圆半径 h-高

　V=?h(R^2-r^2)

高中数学面积体积公式11-17

　11、直圆锥 r-底半径 h-高

　V=?r^2h/3

　12、圆台

　r-上底半径 ，R-下底半径 ，h-高 V=?h(R2+Rr+r2)/3

　13、球

　r-半径 d-直径

　V=4/3?r^3=?d^3/6

　14、球缺

　h-球缺高，r-球半径，a-球缺底半径

　V=?h(3a2+h2)/6 =?h2(3r-h)/3

　15、球台

　r1和r2-球台上、下底半径 h-高

　V=?h[3(r12+r22)+h2]/6

　16、圆环体

　R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径

　V=2?2Rr2 =?2Dd2/4

　17、桶状体

　D-桶腹直径 d-桶底直径 h-桶高

　V=?h(2D2+d2)/12 ，(母线是圆弧形,圆心是桶的中心)

　V=?h(2D2+Dd+3d2/4)/15 (母线是抛物线形)

猜你喜欢：

1. 2017高考数学必考公式大全

2. 高中数学曲线公式

3. 高中数学知识点总结及公式大全

4. 2017年高考必备文科数学公式

5. 高中数学公式排列组合

6. 高中数学几何公式知识

贵州历年高考分数线

　2017年高考已经结束了，那么2017年高考总分多少分?各科的总分都是多少?下面是我整理的2017年各省高考总分，希望能给大家带来帮助!

　 2017年各省高考总分

　就全国的形式来讲，大部分地区的总分值还是一样的，如：安徽、北京、福建、甘肃、广东、广西、贵州、河北、河南、黑龙江、湖北、湖南、吉林、江西、辽宁、内蒙、宁夏、青海、山东、山西、陕西、四川、天津、西藏、新疆、云南、重庆等27个省市还是750分满分。各科的分值详情如下：语文150分，数学150分，英语150分，文综/理综300分。

　个别改革地区的分值详情需要大家做详细的了解，比如江苏、上海、浙江和海南这4个地区：

　浙江地区的高考总分：

　上海和浙江地区2017年采用的是3+3考试模式，即3门必考科目(语文、数学、英语)+选考科目，我们先来看浙江地区的总分：

　其中语文、数学和外语三科满分各为150分，其中英语笔试满分120分，英语听力考试满分30分;综合(文/理)满分300分;自选模块满分60分;技术满分100分，由通用技术和信息技术两科目成绩按各占50%的比例合成。

　需要特别提醒大家的是浙江的总分根据大家的选择而有所差异，即考生文化成绩总分按报考(含兼报)的不同考试类别分别合成。文理科一类为“3+综合+自选模块”的总分，满分为810分;二类为“3+综合”的总分，满分为750分;三类为“3+技术”的总分，满分为550分。

　上海地区的高考总分：

　2017年上海高考成绩满分660分，各科的分值详情是这样的哦：语文、数学(文/理)、外语满分均为150分，政治、历史、地理、物理、化学、生物任选3门：每门70分。

　 江苏地区的高考总分：　　

　江苏同样采用的是必考+选考模式，其中统考科目为语文、数学、外语三门，各科分值设定为：语文160分，数学160分，外语120分，共440分。语文、数学分别另设附加题40分，总分480分。

　选测科目各科满分为120分，按考生成绩分布分为A+、A、B+、B、C、D六个等级。

　 海南地区的高考总分：

　2017年海南的总分以900分的满分当之无愧的位据全国首位，语文、数学(文)、数学(理)、英语等科目的满分值均为150分，其中，英语科分听力和笔试两部分，笔试部分满分值为120分，听力部分满分值为30分，听力成绩计入英语科总分。政治、历史、地理、物理、化学、生物等科目的满分值均为100分，

2017年全国一卷数学高考题，如图，答案最后为什么写m＞负一？

贵州历年高考分数线如下：

2020年： 理科 本科一批 480，理科 本科二批 384、理科 专科批 180、文科 本科一批 548、文科 本科二批 463、文科 专科批 180。

2019年： 理科 本科一批 470、理科 本科二批 369、 理科 专科批 180、理科 体育类（本科） 308、理科 体育类（高职专科） 160、文科 本科一批 542、文科 本科二批 453、文科 专科批 180、文科 体育类（本科） 403、 文科 体育类（高职专科） 160。

2018年： 理科? 本科一批? 484、理科 本科二批 379、理科 专科批 200 、文科 本科一批 575、文科 本科二批 477 、文科 专科批 200 。

2017年： 理科 本科一批 456、理科 本科二批 361、 理科 专科批 200、文科 本科一批 545、文科 本科二批 453、文科 专科批 200。

高考现行方案：3+X方案

“3”指“语文、数学、外语”，“X”指由学生根据自己的意愿，自主从文科综合（简称文综，分为思想政治、历史、地理）和理科综合（简称理综，分为物理、化学、生物）2个综合科目中选择一个作为考试科目。该方案是到2019年全国应用最广。

由前面推导可知，即由题设可知根的判别式=16(4K^2-m^2+1)>0，后面又求得k=-(m+1)/2

这样将k代入进去，4K^2-m^2+1>0

4ⅹ[-(m+1)/2]^2-m^2+1>0

化简得2m+2>0得m>-1

所以当且仅当m>-1时，根的判别式﹥0就是这样得来的。