高考数学题型归纳分析,高考数学题型归纳

1.高中数学经典大题题型 高考数学高频考点归纳

2.高考数学题型与技巧是什么？

3.高考数学常考必考题型是什么？

4.高考数学六道大题是什么题型

5.高考数学题型分布情况如何？

高考数学大题6大题型是：

1、三角函数、向量、解三角形

(1)三角函数画图、性质、三角恒等变换、和与差公式。

(2)向量的工具性(平面向量背景)。

(3)正弦定理、余弦定理、解三角形背景。

(4)综合题、三角题一般用平面向量进行“包装”，讲究知识的交汇性，或将三角函数与解三角形有机融合。

重视三角恒等变换下的性质探究，重视考查图形图像的变换。

2、概率与统计

(1)古典概型。

(2)茎叶图。

(3)直方图。

(4)回归方程。

(5)(理)概率分布、期望、方差、排列组合。概率题贴近生活、贴近实际，考查等可能 性事件、互斥事件、独立事件的概率计算公 式，难度不算很大。

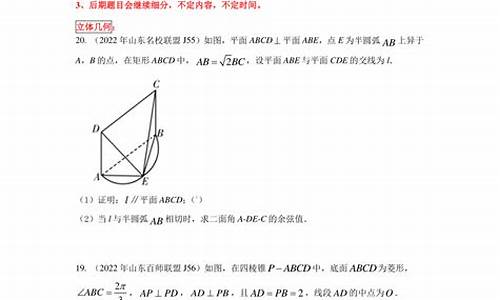
3、立体几何

(1)平行。

(2)垂直。

(3)角。

(4)利用三视图计算面积与体积。

(5)既可以用传统的几何法，也可以建立空间直角坐标系，利用法向量等。

4、数列

(1)等差数列、等比数列、递推数列是考查的热点，数列通项、数列前n项的和以及二者之间的关系。

(2)文理科的区别较大，理科多出现在压轴题位置的卷型，理科注重数学归纳法。

(3)错位相减法、裂项求和法。

(4)应用题。

5、圆锥曲线(椭圆)与圆

(1)椭圆为主线，强调圆锥曲线与直线的位置关系，突出韦达定理或差值法。

(2)圆的方程，圆与直线的位置关系。

(3)注重椭圆与圆、椭圆与抛物线等的组合题。

6、函数、导数与不等式

(1)函数是该题型的主体：三次函数，指数函数，对数函数及其复合函数。

(2)函数是考查的核心内容，与导数结合，基本题型是判断函数的单调性，求函数的最 值(极值)，求曲线的切线方程，对参数取值范 围、根的分布的探求，对参数的分 类讨论以及代数推理等等。

(3)利用基本不等式、对勾函数性质。

高中数学经典大题题型 高考数学高频考点归纳

高考数学参数方程是一种常见的数学题型，它通常涉及一些具有特定参数的方程或不等式，要求考生根据参数的范围或条件来求解方程或不等式的解。

以下是一些高考数学参数方程题型的解题思路和方法：

1.了解参数的意义和作用：在解决参数方程问题之前，首先需要了解参数的意义和作用。参数通常是一种用来描述某个问题或者某种关系的数值或变量，它可以是数字、字母或者其他数学对象。在参数方程中，参数通常会出现在方程的系数、指数、根式等位置，对于不同位置的参数需要进行分类讨论，明确参数的范围和作用。

2.选择适当的参数方程形式：在解决参数方程问题时，需要根据具体问题选择适当的参数方程形式。常见的参数方程形式包括一元二次方程、一元高次方程、二元二次方程组、指数方程、对数方程等。在选择参数方程形式时，需要考虑方程的特点、参数的范围和作用，以及具体的解题需求。

3.利用参数的限制条件：在参数方程问题中，参数通常受到一些限制条件，如参数的范围、取值方式等。在解题时，需要充分利用这些限制条件，缩小参数的范围或者确定参数的值。同时，还需要注意参数的取值是否具有实际意义，避免出现不符合实际的解。

4.分类讨论：在解决参数方程问题时，经常需要对参数进行分类讨论，以确定不同情况下的解。分类讨论可以按照参数的取值范围、方程的形式、方程的性质等特点进行分类，需要注意分类的完整性、分类的合理性和不重不漏的原则。

5.转化和化简：在解决参数方程问题时，经常需要对方程进行转化和化简。转化和化简的目的是将复杂的方程转化为简单的形式，或者将多个方程转化为一个简洁的表达式。在转化和化简过程中，需要注意符号、根式、指数等细节问题，避免出现错误。

6.求解方程或不等式的解：在解决参数方程问题时，最终目的是求解方程或不等式的解。在求解过程中，需要根据具体的问题选择适当的求解方法，如因式分解、求根公式、不等式求解等。同时，还需要注意解的存在性、唯一性、合理性等问题，避免出现不符合实际的解。

高考数学题型与技巧是什么？

对于高考数学来说，想要拿到高分，就需要了解数学中的高频考点，这样才能够提高分数，我为大家整理了一些。

1. 掌握分类计数原理与分步计数原理，并能用它们分析和解决一些简单的应用问题。

2. 理解排列的意义，掌握排列数计算公式，并能用它解决一些简单的应用问题。

3. 理解组合的意义，掌握组合数计算公式和组合数的性质，并能用它们解决一些简单的应用问题。

4. 掌握二项式定理和二项展开式的性质，并能用它们计算和证明一些简单的问题。

5. 了解随机事件的发生存在着规律性和随机事件概率的意义。

6. 了解等可能性事件的概率的意义，会用排列组合的基本公式计算一些等可能性事件的概率。

7. 了解互斥事件、相互独立事件的意义，会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率。

8. 会计算事件在n次独立重复试验中恰好发生k次的概率。

数列是高中数学的重要内容，又是学习高等数学的基础。高考对本章的考查比较全面，等差数列，等比数列的考查每年都不会遗漏。有关数列的试题经常是综合题，经常把数列知识和指数函数、对数函数和不等式的知识综合起来，试题也常把等差数列、等比数列，求极限和数学归纳法综合在一起。探索性问题是高考的热点，常在数列解答题中出现。本章中还蕴含着丰富的数学思想，在主观题中着重考查函数与方程、转化与化归、分类讨论等重要思想，以及配方法、换元法、待定系数法等基本数学方法。

近几年来，高考关于数列方面的命题主要有以下三个方面;(1)数列本身的有关知识，其中有等差数列与等比数列的概念、性质、通项公式及求和公式。(2)数列与其它知识的结合，其中有数列与函数、方程、不等式、三角、几何的结合。(3)数列的应用问题，其中主要是以增长率问题为主。试题的难度有三个层次，小题大都以基础题为主，解答题大都以基础题和中档题为主，只有个别地方用数列与几何的综合与函数、不等式的综合作为最后一题难度较大。

高考数学常考必考题型是什么？

可以是：

一、数列题

1、证明一个数列是等差（等比）数列时，最后下结论时要写上以谁为首项，谁为公差（公比）的等差（等比）数列。

2、最后一问证明不等式成立时，如果一端是常数，另一端是含有n的式子时，一般考虑用放缩法。如果两端都是含n的式子，一般考虑数学归纳法，如何把当前的式子转化到目标式子，一般进行适当的放缩。

3、证明不等式时，有时构造函数，利用函数单调性很简单，所以要有构造函数的意识。

二、立体几何题

1、证明线面位置关系，一般不需要去建系，更简单。

2、求异面直线所成的角、线面角、二面角、存在性问题、几何体的高、表面积、体积等问题时，最好要建系。

3、注意向量所成的角的余弦值（范围）与所求角的余弦值（范围）的关系（符号问题、钝角、锐角问题）。

三、概率问题

1、搞清随机试验包含的所有基本事件和所求事件包含的基本事件的个数。

2、搞清是什么概率模型，套用哪个公式。

3、记准均值、方差、标准差公式。

4、注意计数时利用列举、树图等基本方法。

5、注意放回抽样，不放回抽样。

6、注意零散的知识点（茎叶图、频率分布直方图、分层抽样等）在大题中的渗透。

四、圆锥曲线问题

1、注意求轨迹方程时，从三种曲线（椭圆、双曲线、抛物线）着想，椭圆考得最多，方法上有直接法、定义法、交轨法、参数法、待定系数法。

2、注意直线的设法，知道弦中点时，往往用点差法，注意自变量的取值范围。

高考数学六道大题是什么题型

高考数学常考的大题分别是三角函数或数列，概率，立体几何，解析几何(圆锥曲线)，函数与导数。

高考数学必考知识点归纳：

必修一：集合与函数的概念（部分知识抽象，较难理解）；基本的初等函数（指数函数、对数函数)；函数的性质及应用（比较抽象，较难理解）。

必修二：立体几何、证明：垂直（多考查面面垂直）、平行求解：主要是夹角问题，包括线面角和面面角。

这部分知识是高一学生的难点，比如：一个角实际上是一个锐角，但是在图中显示的钝角等等一些问题，需要学生的立体意识较强。这部分知识高考占22---27分。

2、直线方程：高考时不单独命题，易和圆锥曲线结合命题。

3、圆方程。

平面向量：高考不单独命题，易和三角函数、圆锥曲线结合命题。09年理科占到5分，文科占到13分。

文科：选修1—1、1—2。

选修1--1：重点：高考占30分。

1、逻辑用语：一般不考，若考也是和集合放一块考；2、圆锥曲线；3、导数、导数的应用（高考必考）。

选修1--2：1、统计；2、推理证明：一般不考，若考会是填空题；3、复数：（新课标比老课本难的多，高考必考内容）。

理科：选修2—1、2—2、2—3。

选修2--1：1、逻辑用语;2、圆锥曲线;3、空间向量：（利用空间向量可以把立体几何做题简便化）。

选修2--2：1、导数与微积分；2、推理证明：一般不考3、复数。

选修2--3：1、计数原理：（排列组合、二项式定理）掌握这部分知识点需要大量做题找规律，无技巧。高考必考，10分；2、随机变量及其分布：不单独命题；3、统计。

高考数学题型分布情况如何？

高考数学六道大题的题型是：三角函数，概率，立体几何，函数，数列，解析几何。

1、三角函数。是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。

2、概率。它是反映随机事件出现的可能性大小。随机事件是指在相同条件下，可能出现也可能不出现的事件。

3、立体几何。是3维欧氏空间的几何的传统名称，因为实际上这大致上就是我们生活的空间。一般作为平面几何的后续课程。

4、函数。数学术语。其定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。

5、数列。是以正整数集（或它的有限子集）为定义域的一列有序的数。数列中的每一个数都叫做这个数列的项。

6、解析几何。是一种借助于解析式进行图形研究的几何学分支。

学习数学重要性：

1、数学与我们生活息息相关。要说学数学的真正效果，它不是体现在应试教育上，而是将来自身的思维上。

2、数学的重要性不言而喻。数学是一切科学的基础，是培养逻辑思维重要渠道，可以说我们人类的每一次重大进步都有数学这门学科在做强有力的支撑。

3、生活中的数学知识运用无处不在。从日常生活中柴米油盐的费用的计算，到天文地理、质量控制、农业经济、航天事业都存在着运用数学的影子。

高考数学题型分布情况一般是根据各省份高考的具体要求和考题情况而定，不同省份会有一定的差异，但总体来说，高考数学的题型主要包括以下几个方面：

选择题：选择题通常涉及到基本的数学知识点和计算技能，如运算、代数、几何、概率等。

填空题：填空题通常要求考生根据题目提供的信息，推导出答案并填入相应的空格中。

解答题：解答题通常是要求考生结合所学的数学知识，对一些较为复杂的问题进行分析和解答。

计算题：计算题主要是要求考生对所学的数学知识进行灵活运用，解决一些需要进行复杂计算的问题。

在各省份高考数学试卷中，以上四种题型的分布情况可能会有所不同，但大多数试卷会保持相对平衡，注重考查学生的数学思维能力和解决实际问题的能力。