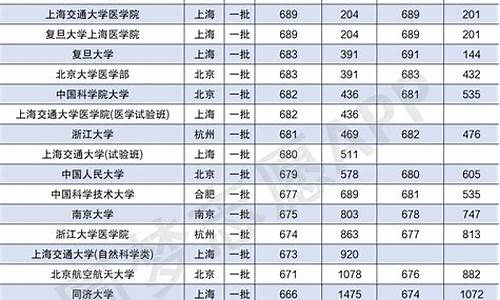
您现在的位置是: 首页 > 教育政策 教育政策
高考文科数学难度系数_高考文数难易
tamoadmin 2024-05-15 人已围观
简介高考全国卷难易程度排行:全国卷难度排名是全国一卷最难,全国二卷次之,全国三卷最简单。全国卷分3套卷子考试,使用全国一卷的省份,高考时考试科目及各科试题是完全一样的,但是高考分数线各省不同。类似的,使用全国2卷和使用全国3卷的省份各自的试题也是一样的。全国卷123区别主要在于使用省份的区别,在难度系数上,三套卷差距不是很大。一般情况下是全国1卷和2卷要比全国3卷难度高一些。高考难度地区排名1、高考难

高考全国卷难易程度排行:全国卷难度排名是全国一卷最难,全国二卷次之,全国三卷最简单。
全国卷分3套卷子考试,使用全国一卷的省份,高考时考试科目及各科试题是完全一样的,但是高考分数线各省不同。类似的,使用全国2卷和使用全国3卷的省份各自的试题也是一样的。全国卷123区别主要在于使用省份的区别,在难度系数上,三套卷差距不是很大。一般情况下是全国1卷和2卷要比全国3卷难度高一些。
高考难度地区排名
1、高考难度一颗星:北京、上海、天津。
这些地区的高考难度在全国来说是最低的。首先,这些地区参加高考的人数相对比较少。另外,这三个地区是我们国内教育资源最集中的地区,拥有很多所名牌大学。大学招生对于本地考生都有一定的政策倾斜,这也意味着在这三个地区考上大学相对于其他地区会容易很多。
2、高考难度两颗星:吉林、西藏、宁夏、辽宁、青海。
首先,这五个省份的高考试卷难度是相对比较简单的。此外,这五个省份每年的高考人数每年在全国都是比较少的,尤其是青海和西藏,这两个省份的高考人数至少可以排进我们国内前五。
3、高考难度三颗星:湖北、陕西、黑龙江、内蒙古、海南、新疆。
这七个省份的高考试卷难度是普通难度,高考人数也是处于中等水平。此外,这几个地区每年的高校录取率也是比较中规中矩的,比如说985录取率,这几个地区处于全国平均水平,大约为1.62%左右。
4、高考难度四颗星:甘肃、云南、四川、贵州、湖南、河北、重庆、山西、山东、广西、安徽。
这些省份高考人数比较多,不论本科录取率还是211、988大学录取率都比较低,竞争压力也比较大,这些地区的高考难度都是比较高的。
5、高考难度五颗星:江西、江苏、广东、浙江、河南。
广东省和河南省基本每年的高考人数都是全国最多的。尤其河南省每年都有上百万的考生,而省内却连一所985大学都没有,只有一所211大学,想考名校的难度是非常大的。江西省分数线在逐年升高,而全国各大学在江西省的投放名额却非常少,这也导致了江西省一本录取率是非常低的。
文科数学和理科数学高考题有一部分是相同的,而其余题目则有所差别,难度具体差二三十分左右,因人而异。理科数学题目比文科数学深,考查范围广,具体可以看考试大纲。
高考数学卷的文理差异
文科生会不会吃亏?沪上某区数学教研员给出了否定的回答。他分析说,上海二期课改高中数学教材共有18章是公共部分,有5个专题属于文理分叉,“学生从高一到高三上学期,基本上学的都是公共部分。尤其是高一、高二阶段,数学可以说没有文理之分,学生也在这两年中基本掌握了必要的数学素养。”
那么,高考数学文理卷差别究竟在哪?该教研员解释说,文理卷的差别首先体现在分叉部分,如文科生学三视图,理科生就不用。理科生要学极坐标、参数方程,对文科生却不作要求。差别二是针对公共部分,对文理科学生思维层次的要求不同。在这位老师看来,思维层次分三个,记忆性层次、理解性层次和探究性层次。如果新的课程标准出台后,将数学考试的难度定位在记忆性和理解性水平上,那文科生的负担就不会加重。
高考文理科数学难度不同
文理科数学即使是针对同一个考察点的考察,难度也是有很大不同的。对于基础题目文理科数学一般都是一样的。主要的差别在于一些中高档题目上。
文科题目的已知条件往往比理科题目直接,从而容易解答。另外理科有一些知识点文科是没有的,不过这个比较少。而且理科的数学要求高些,所学的知识有部分比文科更深入。所以从难易程度看,高考理科数学要难于高考文科数学。
文科理科数学差很多吗
文科函数部分:定积分、复合函数的导数、导数的几何意义不考;函数次数不能超过三次;立体几何部分:空间向量、向量方法都不考;角度只要求直线与平面的,不要求异面直线和二面角;圆锥曲线部分:直线与圆锥曲线、曲线方程都不考;浙江文科考查直线与抛物线关系概率部分:计数原理、二项式、离散型、正态分布、几何概率都不考;数学归纳法不考;
(1)理科:理解两条异面直线所成角、直线与平面所成角、二面角的概念文科:了解两条异面直线所成角及二面角的概念,理解并会求直线与平面所成角。
(2)理科:能用坐标法解决简单的直线与椭圆、抛物线的位置关系等问题。文科:能用坐标法解决简单的直线与抛物线的位置关系等问题。
(3)理科:了解方程的曲线与曲线的方程的对应关系。文科:无
(4)理科:空间向量与立体几何(整大块)文科:无
(5)理科:导数概念及其几何意义1.了解导数概念的实际背景。2.理解导数的几何意义。文科:无
(6)理科:无特别提示的限制文科:1.了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(对多项式函数不超过三次)。2.了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(对多项式函数不超过三次);会求闭区间上函数的最大值、最小值(对多项式函数不超过三次)。
(7)理科:数学归纳法:了解数学学归纳法的原理,能用数学归纳法证明一些简单的数学命题。文科:无
(8)理科:计数原理。文科:框图
(9)理科:能求简单的复合函数(仅限于形如f(ax+b))的导数。文科:无