高考函数问题概括_高考函数问题

1.高三文科数学三角函数题~！求助！！~急急急！！！

2.如图。高三三角函数的分拆问题

3.求教一个三角函数的证明问题,高三,谢谢

4.二次函数大题(高三)

5.函数的问题，高三的题，感觉跟大学的凹凸函数有点关系

6.高考数学函数答题方法和技巧

1.因为：g(x)=1+2/(2^x-1)

=(2^x+1)/(2^x-1)

所以：g(-x)=-(2^x+1)/(2^x-1)=-g(x)

所以g(x)是奇函数

奇函数乘以奇函数等于偶函数 所以f(x)是偶函数 选择B

2.依题，距离最小值就是圆心到直线的距离减去圆的半径画图可以很轻松的看出来

而圆心（0，0）到直线距离为：

d=|0+0-25|/根号(3^2+4^2)=5

所以距离最小值为5-1=4

高三文科数学三角函数题~！求助！！~急急急！！！

解：f(x)=√3sinwx+coswx=2sin（wx+π/6）

∵该函数图像与直线y=2的两个相邻交点的距离等于π

∴该函数周期T=π=2π/w

∴w=2

∴f（x）=2sin（2x+π/6）

令-π/2+2kπ≤2x+π/6≤π/2+2kπ

k∈Z

得：kπ-π/3≤2x+π/6≤kπ+π/6

k∈Z

答案应该为C

如图。高三三角函数的分拆问题

由余弦定理可知2accosB=a^2+c^2-b^2；2abcosc=a^2+b^2-c^2；

代入3acosA=ccosB+bcosC；

得cosA=1/3 ；

∴sinA= 2√3/3

cosB=-cos（A+C）=-cosAcosC+sinAsinC=-1/3 cosC+ 2√3/3 sinC ③

又已知 cosB+cosC= 2√3/3 代入 ③

cosC+√2 sinC=√3 ，与cos^2C+sin^2C=1联立

解得 sinC= √6/3

已知 a=1

正弦定理：c= √3/2

求教一个三角函数的证明问题,高三,谢谢

∵函数f(x)=Asin(wx+φ)（w＞0,|φ|<π/2），M(-1,0)，N(1,1)，P(5,-1)

由图可知A=1，T/2=5-1=4==>T=8==>w=2π/8=π/4

∴f(x)=sin(π/4x+φ)==> π/4x+φ=π/2==>x=2(π-2φ)/π

2(π-2φ)/π=1==>φ=π/4

∴f(x)=sin(π/4x+π/4)

MN的斜率k1=1/2，NP的斜率k2=-1/2

二直线夹角的正切值=(k2-k1)/(1+k1k2)=-4/3

∴tan∠MNP=-4/3==>sin∠MNP=4/5

二次函数大题(高三)

左边 分子可以 写成[sinx+(cosx-1)][sinx-(cosx-1)]

利用平方差公式 得 sinx平方-（cosx-1）平方 化简得2cosx-2（cosx）平方，

分母可用2倍角公式写成 2 sinx cosx. 约分得sinx 分之（1-cosx）

.再利用 半角公式：

cosx=1-（cos二分之X）平方。

所以 1-cosx =cos二分之X平方 。

sinx=2sin二分之x 乘以cos二分之x

约分得 左边= sin二分之x / cos二分之x ，即等于tan二分之x

左边 =右边 ，故上式成立

函数的问题，高三的题，感觉跟大学的凹凸函数有点关系

不等式变形为π^[f(x)]>1/π^(2-tx)，即π^[f(x)+(2-tx)]＞1=π^0，因为π＞1，所以f(x)+(2-tx)]＞0

得(1/2)x?-（t-1）x+2＞0

看成t的不等式，即（1/2）x?+x+2＞xt，当x＞0时t＜（1/2）x+1+2/x，于是（1/2）x+1+2/x＞2大于最大值，显然恒成立。当x=0时不等式成立

当x＜0时t＞（1/2）x+1+2/x，于是（1/2）x+1+2/x＜-2小于最小值，得x＜-3-根号5。

综上，x的范围是x＜-3-根号5或x≥0

高考数学函数答题方法和技巧

解决两个问题就可以了。

1、μx1+(1-μ)x2：考虑下定比分点；

2、2f[μx1+(1-μ)x2]≤μf(x1)+(1-μ)f(x2)：其实这个式子表示的真正含义是“分点时的函数值小于等于两端函数值的和”，你的想法是可靠的，的确和函数的凹凸性有关。此函数应该满足凹函数或一次函数(因为有等于号)。

3、满足的条件是不是“2f[μx1+(1-μ)x2]≤μf(x1)+(1-μ)f(x2)”

答案：1和3都可以的。

#高三# 导语怎么答好高考数学函数题？ 整理了高考数学函数题答题技巧和方法，供参考。

　 高考函数体命题方向

　高考函数与方程思想的命题主要体现在三个方面

　①是建立函数关系式，构造函数模型或通过方程、方程组解决实际问题;

　②是运用函数、方程、不等式相互转化的观点处理函数、方程、不等式问题;

　③是利用函数与方程思想研究数列、解析几何、立体几何等问题.在构建函数模型时仍然十分注重“三个二次”的考查.特别注意客观形题目，大题一般难度略大。

　 高考数学函数题答题技巧

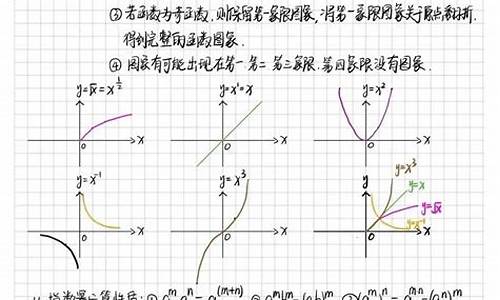
　对数函数

　对数函数的一般形式为，它实际上就是指数函数的反函数。因此指数函数里对于a的规定，同样适用于对数函数。

　对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形，因为它们互为反函数。

　(1)对数函数的定义域为大于0的实数集合。

　(2)对数函数的值域为全部实数集合。

　(3)函数总是通过(1，0)这点。

　(4)a大于1时，为单调递增函数，并且上凸;a小于1大于0时，函数为单调递减函数，并且下凹。

　(5)显然对数函数无界。

　指数函数

　指数函数的一般形式为，从上面我们对于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得

　可以得到：

　(1)指数函数的定义域为所有实数的集合，这里的前提是a大于0，对于a不大于0的情况，则必然使得函数的定义域不存在连续的区间，因此我们不予考虑。

　(2)指数函数的值域为大于0的实数集合。

　(3)函数图形都是下凹的。

　(4)a大于1，则指数函数单调递增;a小于1大于0，则为单调递减的。

　(5)可以看到一个显然的规律，就是当a从0趋向于无穷大的过程中(当然不能等于0)，函数的曲线从分别接近于y轴与x轴的正半轴的单调递减函数的位置，趋向分别接近于y轴的正半轴与x轴的负半轴的单调递增函数的位置。其中水平直线y=1是从递减到递增的一个过渡位置。

　(6)函数总是在某一个方向上无限趋向于x轴,永不相交。

　(7)函数总是通过(0，1)这点。

　(8)显然指数函数无界。

　奇偶性

　一般地，对于函数f(x)

　(1)如果对于函数定义域内的任意一个x，都有f(-x)=-f(x)，那么函数f(x)就叫做奇函数。

　(2)如果对于函数定义域内的任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。

　(3)如果对于函数定义域内的任意一个x，f(-x)=-f(x)与f(-x)=f(x)同时成立，那么函数f(x)既是奇函数又是偶函数，称为既奇又偶函数。

　(4)如果对于函数定义域内的任意一个x，f(-x)=-f(x)与f(-x)=f(x)都不能成立，那么函数f(x)既不是奇函数又不是偶函数，称为非奇非偶函数。

　说明：①奇、偶性是函数的整体性质，对整个定义域而言

　②奇、偶函数的定义域一定关于原点对称，如果一个函数的定义域不关于原点对称，则这个函数一定不是奇(或偶)函数。

　(分析：判断函数的奇偶性，首先是检验其定义域是否关于原点对称，然后再严格按照奇、偶性的定义经过化简、整理、再与f(x)比较得出结论)

　③判断或证明函数是否具有奇偶性的根据是定义

　 函数的性质与图象

　函数的性质是研究初等函数的基石，也是高考考查的重点内容．在复习中要肯于在对定义的深入理解上下功夫．

　复习函数的性质，可以从“数”和“形”两个方面，从理解函数的单调性和奇偶性的定义入手，在判断和证明函数的性质的问题中得以巩固，在求复合函数的单调区间、函数的最值及应用问题的过程中得以深化．具体要求是：

　1．正确理解函数单调性和奇偶性的定义，能准确判断函数的奇偶性，以及函数在某一区间的单调性，能熟练运用定义证明函数的单调性和奇偶性．

　2．从数形结合的角度认识函数的单调性和奇偶性，深化对函数性质几何特征的理解和运用，归纳总结求函数值和最小值的常用方法．

　3．培养学生用运动变化的观点分析问题，提高学生用换元、转化、数形结合等数学思想方法解决问题的能力．

　这部分内容的重点是对函数单调性和奇偶性定义的深入理解．

　函数的单调性只能在函数的定义域内来讨论．函数y＝f(x)在给定区间上的单调性，反映了函数在区间上函数值的变化趋势，是函数在区间上的整体性质，但不一定是函数在定义域上的整体性质．函数的单调性是对某个区间而言的，所以要受到区间的限制．

　对函数奇偶性定义的理解，不能只停留在f(－x)＝f(x)和f(－x)＝－f(x)这两个等式上，要明确对定义域内任意一个x，都有f(－x)＝f(x)，f(－x)＝－f(x)的实质是：函数的定义域关于原点对称．这是函数具备奇偶性的必要条件．稍加推广，可得函数f(x)的图象关于直线x＝a对称的充要条件是对定义域内的任意x，都有f(x＋a)＝f(a－x)成立．函数的奇偶性是其相应图象的特殊的对称性的反映．

　这部分的难点是函数的单调性和奇偶性的综合运用．根据已知条件，调动相关知识，选择恰当的方法解决问题，是对学生能力的较高要求．