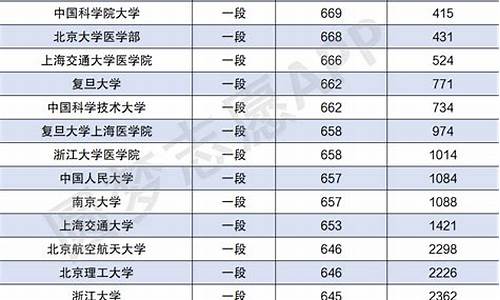
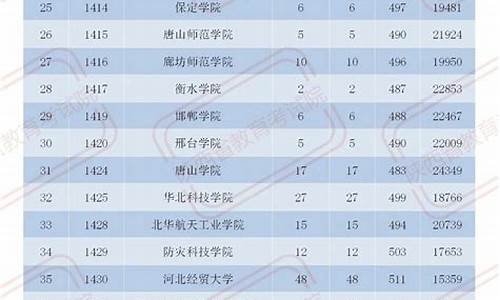
您现在的位置是: 首页 > 招生信息 招生信息
2024高考导数题,2024高考导数
tamoadmin 2024-06-10 人已围观
简介1.导数公式高考会给出吗2.高考怎样轻松应对导数3.新高考数学导数难度下降原因4.高考数学导数大题怎么确保思路正确 什么是偏导数偏导数是指在多元函数中,固定其他变量而只对一个特定变量求导数的方法。例如,对于函数f(x,y)=xy,当我们对x求偏导时,就是把y当作常数,结果就是y。 如何求偏导数对于题目中的?x*?y,我们需要先对y求偏导,然后再对x求偏导。具体的读法是“对什么什么求偏导”,这样
1.导数公式高考会给出吗
2.高考怎样轻松应对导数
3.新高考数学导数难度下降原因
4.高考数学导数大题怎么确保思路正确

什么是偏导数
偏导数是指在多元函数中,固定其他变量而只对一个特定变量求导数的方法。例如,对于函数f(x,y)=xy,当我们对x求偏导时,就是把y当作常数,结果就是y。
如何求偏导数对于题目中的?x*?y,我们需要先对y求偏导,然后再对x求偏导。具体的读法是“对什么什么求偏导”,这样可以更好地理解偏导数的概念。
如何理解偏导数偏导数是多元函数中的一种求导方法,它可以帮助我们在多个变量的函数中,固定其他变量而只对一个特定变量求导数。通过理解偏导数的概念,我们可以更好地应用它来解决实际问题。
导数公式高考会给出吗
2022年高考数学评分细则如下:
针对导数第三问,由于网上传出来的qhf事件,第三问实际上只给了4分,第一问第二问分数有所提升,这可能也是教委保护我们的方式吧...实际上一个正常的高中生也应该能写出来前两问,也已经能拿大部分分数了,最后加和到卷面上也会是不难看的成绩。
针对立体几何建系需要严谨证明的问题,还是由于今年考题难度太大,判卷方面也放了水。写出来严谨的建系证明那部分给满分4分。如果没写,没有用题目给的条件也给了足足三分。针对椭圆,只要联立了就给分,不管联立的对不对都给分。两根之和两根之积同样也是。
针对压轴题,第一问给了4分,第二问给了5分。这个分数给的算是合理,但第二问的证明其实也是比较水的。只要证明当k=3的时候没有八个数,然后举例证明当k=4的时候可以,这个五分基本上就拿到手了。
学数学好处
数学好的人,相对比较聪明,领悟力较高,在对人处事上能体现出优势。思维比较敏捷,方法点子会较多。数学是其他学科的基础,学好数学的人,对于其他学科更容易上手。学软件、计算机、金融等工科专业就更是得心应手。
在生活中的运用无处不在,现在的社会已经是信息社会,金融理财、计算机等都要用到数学知识。数学可以培养人正直与诚实的品质。数学最讲究以理服人,它只信奉逻辑推理的结果。数学可以培养人的顽强与勇气。数学可以培养人的整体意识。数学可以培养人的良好性格。
高考怎样轻松应对导数
会。导数公式高考会给出,导数是高考数学的重点,同时也是难点,在高考中重点考查。导数(Derivative)是微积分中的重要基础概念。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
新高考数学导数难度下降原因
导数是高中数学重点内容之一,同学们在复习时应注意导数的工具性作用,扣紧这一重点,切实掌握导数在解决导数在解决函数问题时的应用方法,学会用数学思想和方法寻求规律找出解决策略。 下面是对高考中考察导数和函数知识的总结。 1.考察函数定义域 2.考察函数解析式 3.考察反函数 4.考察函数的奇偶性,单调性 5.考察函数图像及性质 6.考察导数的几何意义 7.考察导数研究函数的单调性和极值 寻找其中的重点并且紧扣这些知识,认真准备应用试题,重视函数的数学模型问题。
此外多练导数题,多总结,到最后会有收获的。
高考数学导数大题怎么确保思路正确
难度大。导数的几何意义理解不完整,极值、极值点、取得极值时的点概念混淆,取得极值的条件不清楚。常规而言,一套高考数学题中的曲锥曲线和导数题是最难的,导数,也叫导函数值。又名微商,是微积分中的重要基础概念。
高考导数考什么?
高考导数题主要是考查与函数的综合,考查不等式、导数的应用等知识,难度属于中等难度。
都有什么题型呢?
①应用导数求函数的单调区间,或判定函数的单调性;
②应用导数求函数的极值与最值;
③应用导数解决有关不等式问题。
有没有什么解题技巧啦?
导数的解题技巧还是比较固定的,一般思路为
①确定函数f(x)的定义域(最容易忽略的,请牢记);
②求方程f′(x)=0的解,这些解和f(x)的间断点把定义 域分成若干区间;
③研究各小区间上f′(x)的符号,f′(x)>0时,该区间为增区间,反之则为减区间。
从这两步开始有分类讨论,函数的最值可能会出现极值点处或者端点处,多项式求导一般结合不等式求参数的取值范围,根据题目会有一定的变化,那接下来具体总结一些做题技巧。
技巧破解+例题拆解
1. 若题目考察的是导数的概念,则主要考察的是对导数在一点处的定义和导数的几何意义,注意区分导数与△y/△x之间的区别。
2. 若题目考察的是曲线的切线,分为两种情况:
(1)关于曲线在某一点的切线,求曲线y=f(x)在某一点P(x,y)的切线,即求出函数y=f(x)在P点的导数就是曲线在该点的切线的斜率.
(2)关于两曲线的公切线 ,若一直线同时与两曲线相切,则称该直线为两曲线的公切线.