您现在的位置是: 首页 > 教育研究 教育研究
高考函数例题,高考函数题型及解题方法
tamoadmin 2024-06-15 人已围观
简介1.高考摸题--函数2.高三函数题3.高三数学函数最值问题4.高三数学函数题5.高三文科函数题目~急求~6.求解高三函数题7.高三试题,要详细过程,急急急: 已知函数f(x)=ax+lnx(a∈R), ①若a=2,求曲线y=f(x)在x...8.2道高考题外加1道函数题第3题这种类型的题的解法是:把sinxcosx化成sinx+cosx的形式,然后设sinx+cosx=t,再根据t的范围求解函数的
1.高考摸题--函数
2.高三函数题
3.高三数学函数最值问题
4.高三数学函数题
5.高三文科函数题目~急求~
6.求解高三函数题
7.高三试题,要详细过程,急急急: 已知函数f(x)=ax+lnx(a∈R), ①若a=2,求曲线y=f(x)在x...
8.2道高考题外加1道函数题
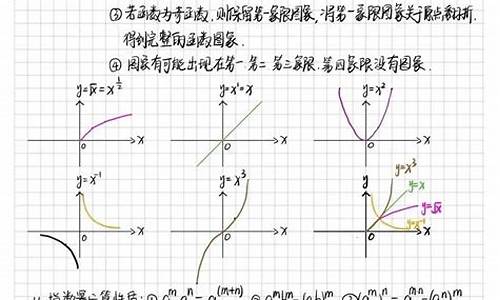
第3题这种类型的题的解法是:
把sinxcosx化成sinx+cosx的形式,然后设sinx+cosx=t,再根据t的范围求解函数的最值,如下:
设t=sinx+cosx
那么t=sinx+cosx
=√2[(√2/2)sinx+(√2/2)cosx]
=√2[cos(π/4)sinx+sin(π/4)cosx]
=√2sin(x+π/4)
∴t∈[-√2,√2]
又∵t?=(sinx+cosx)?
=sin?x+2sinxcosx+cos?x
=1+2sinxcosx
∴sinxcosx=(t?-1)/2
∴y=[(t?-1)/2]+t,t∈[-√2,√2]
抛物线y的对称轴是t=-1
∴t=-1时y(min)=-1;t=√2时y(max)=(√2)+1/2
或者化成完全平方加一个常数的形式:y=(1/2)(t+1)?-1来计算也很容易。
括号打的有点多,怕你误解,相信以你的水平也不会,肯定能看懂的是吧!
总之,对于三角函数的计算要把公式与公式的转化运用的非常熟练,另外做过的题一定要看到题就想到思路,不要过一段时间再回来做就忘的差不多了那样的,到高考会很纠结的。
还有一种解法是求导,不知你们现在高中学了没,反正我们那时候好像没学过积的导数,三角函数的导数公式忘了学过没。。。(sinx)'=cosx;(cosx)'=-sinx
方法如下:(积的导数公式:(uv)'=u'×v+u×v',其中u,v都是x的函数)
y'=(sinx)'cosx+sinx(cosx)'+(sinx)'+(cosx)'
=cos?x-sin?x+cosx-sinx
=(cosx-sinx)(cosx+sinx+1)
=√2cos(x+π/4)[√2sin(x+π/4)+1]
令y'=0,得cos(x+π/4)=0或√2sin(x+π/4)+1=0
得x+π/4=(2m+1)π或x=(2k-1/2)π±π/4
再代入求最值,当然这个比较麻烦点,在某些场合用导数会更简便。
对于三角函数,不到万不得已不要用万能公式,另外你们应该也做过用万能公式的题,也就那些题型记住就行了,其他的看着办。
第5题,看来你基础知识没学好,把高一第一册课本的奇偶函数那一节翻出来看是怎么定义的!
奇函数可以这么理解:定义域关于原点对称,函数图象关于原点对称,对于三角函数来说,在定义域关于原点对称的基础上,只要函数过原点,也就是把点(0,0)代入可以使方程成立那么就是奇函数。
相应地,偶函数是定义域关于原点对称,函数图象关于y轴对称的函数。对于三角函数来说,定义域关于原点对称的基础上,x=0是函数的一个极值点就是偶函数,也就是在图象上x=0的点是最高点或者最低点,或者在x=0处的导数等于0,都是可以用来判定的。
你这个例子,你们老师说把它当整体看,是说括号内整体等于t,那么t=0时cosx取最大值,但是此时x=-9π/4≠0,也就是说x和t不是同一个概念,x=-9π/4才是f(x)的对称轴。反过来看,当x=0时t=9π/2,f(0)=0,也就是过原点,是奇函数。
你所认为的cosx是偶函数,是标准的余弦函数,也就是不平移,不伸缩,但是f(x)是在cosx的基础上平移和伸缩了的,当你把cosx向右平移π/2时就变成了sinx的标准情况,也就是y=cos(x-π/2)是奇函数,所以不能笼统的说以cos开头的函数就是偶函数,还是得求对称轴的。
其他的题应该是比较简单的,我有时间再算,挺忙的。有不懂的再留言!
希望能给你带来帮助。
高考摸题--函数
解:(1)由图像知,函数振幅为2,故A=2
由图像知从-π/3到2π/3是半个周期,故T=[(2π/3-(-π/3)]*2=2π
即2π/ω=2π, 所以ω=1
所以f(x)=2sin(x+φ)
把最高点(2π/3, 2)(或最低点(-π/3,-2))代入函数,得2=2sin(2π/3+φ)
故sin(2π/3+φ)=1
所以2π/3+φ=π/2+2kπ(k∈Z),
即φ=2kπ-π/6(k∈Z)
因为-π/2<φ<π/2
所以φ=-π/6
所以f(x)=2sin(x-π/6)
(2)因f(a)=3/2, 即sin(a-π/6)=3/4
所以sin(2a+π/6)=cos[π/2 -(2a+π/6)](这里利用诱导公式cos(π/2-a)=sina)
=cos(π/3-2a)=cos(2a-π/3)(这里利用诱导公式cos(-a)=cosa)
=cos[2(a-π/6)]=1-2[sin(a-π/6)]^2 (这里利用2倍角公式)
=1-2(3/4)^2=-1/8
即sin(2a+π/6)=-1/8
高三函数题
已知函数f(x)=ln[e^x+a](a为常数)是实数集R上的奇函数,
函数g(x)=λf(x)+sinx是区间[-1,1]上的减函数。
(1)求a的值。
(2)若g(x)≤t?+λt+1在x∈[-1,1]上恒成立,求t的取值范围。
(3)讨论关于x的方程(lnx)/f(x)=x?-2ex+m的根的个数。
(1)f(x)是奇函数--->f(0)=0,即ln(1+a)=0--->a=0
(2)--->f(x)=x--->g(x)=λx+sinx是区间[-1,1]上的减函数
--->g'(x)=λ+cosx≤0在区间[-1,1]上恒成立--->λ≤-1
--->g(x)=λx+sinx在[-1,1]上的最大值=g(-1)=-(λ+sin1)
g(x)≤t?+λt+1在x∈[-1,1]上恒成立即:g(-1)≤t?+λt+1成立
--->t?+λt+(1+λ+sin1)≥0--->λ(t+1)≥-(t?+1+sin1)
∵λ≤-1,∴(t+1)<0且-(t?+1+sin1)/(t+1)≥-1
--->t?+1+sin1≥t+1--->t?-t+sin1≥0,
Δ<0显然成立
--->t<-1
(3)(lnx)/f(x)=x?-2ex+m
高三数学函数最值问题
(1)集合A={x|f(x)=x}={1,2}
表示当f(x)=x,即ax^2+(b-1)x+c=0时,
两根x1,x2分别为1,2
所以由韦达定理得x1+x2=-(b-1)/a=3
x1*x2=c/a=2
再由f(0)=c=2 解得a=1,b=-2,c=2
所以f(x)=x^2-2x+2=(x-1)^2+1
由f(x)图像可知:
m=f(x)min=f(1)=1
M=f(x)max=f(-2)=10
(2)集合A={x|f(x)=x}={2}
表示当f(x)=x,即ax^2+(b-1)x+c=0时,
只有唯一的一个根x=2
所以得△=(b-1)^2-4ac=0
且x=-b/2a=2
代入得b=-4a ,c=[(b-1)^2]/4a=4a+1/(4a)+2
则f(x)=ax^2-4ax+4a+1/(4a)+2
因为a≥1,所以可以利用基本不等式
得f(x)≥ax^2-4ax+2[√4a*1/(4a)]+2
=ax^2-4ax+4
对称轴x=-b/2a=-(-4a)/2a=2
由f(x)的图像可知:
m=f(X)min=f(2)=-4a+4
M=f(x)max=f(-2)=12a+4
则 g(a)=M+m=8a+8 (a≥1)
由g(a)的图像可知:g(a)在[1,+∞)上单调递增
所以g(a)min=g(1)=8*1+8=16
高三数学函数题
解:f(x)=x?-3x+1/(x-1)+3
f'(x)=2x-3-1/(x-1)?
令f'(x)=0得:
2x-3-1/(x-1)?=0
(2x-3)(x-1)?=1
2x?-7x?+8x-4=0
(x-2)(2x?-3x+2)=0
则x=2
∵1<x<2时,f‘(x)<0
x>2时,f'(x)>0
∴fmin=f(2)=4-6+1+3=2
高三文科函数题目~急求~
(I)e^x是单调递增函数,因此只要a>0,f(x)就是单调递增函数;
f(x)只与y轴相交,交点A:x=0,y=a;
g(x)=ln(x/a),只与x轴相交,交点B:x=a,g(x)=0;
OAB是等边直角三角形,|AB|=a√2;
点到曲线的距离,与点到直线的距离意义一样,由该点项曲线作“垂线”,点与垂足的连线就是点到该曲线的距离,这个距离在垂足附近最短。这个“垂线”指的是,距离线与垂足处曲线的切线相互垂直。
|AB|是f(x),g(x)上最短距离,意味着,f(x)在A点的切线,g(x)在B点的切线都垂直于AB,AB斜率kAB=(0-a)/(a-0)=-1,切线斜率k=1
f'(x)=ae^x,f'(x)=a=1,
g'(x)=a/x*(1/a)=1/x
g'(a)=1/a=1
a=1
(II)a=1,不等式成为:(x-m)/lnx≥√x,x>0;√x>0;
x=1时,lnx=0,不等式左边无定义,因此以此点分界,分别讨论:
0<x<1时,lnx<0,但是(x-m)/lnx≥√x>0,因此,x-m<0,m>x,必须有m≥1;
(x-m)≤√xlnx,设z=(x-m)-√xlnx≤0;
z'=1-lnx/2√x-√x/x=1-lnx/2√x-1/√x=1-(0.5lnx+1)/√x=1-(ln√x+1)/√x=1-ln[1/(√x)^(√x)]-1/√x
0<x<1;0<√x<1;1/√x>1;0<(√x)^(√x)<1,1/(√x)^(√x)>1,ln[1/(√x)^(√x)]>0;
因此,z'<0,函数递减,只要x->0时,z<0即可;
x->0时,√xlnx是0*∞型不定式,用洛必达法则,先化成∞/∞型,分子分母分别求导:
√xlnx《=》lnx/x^(-0.5)《=》(1/x)/(-0.5x^(-1.5))=-2√x->0,
x->0时,z->-m<0,m>0即可。
因此:m≥1;
x>1时,lnx>0,x-m≥√xlnx>0,x-m>0,m<x,对于所有x>1,恒成立,因此m≤1.
设z=(x-m)-√xlnx≥0;
z'=1-ln[1/(√x)^(√x)]-1/√x
x>1,√x>1,0<1/√x<1,(√x)^(√x)>1,0<1/(√x)^(√x)<1,ln[1/(√x)^(√x)]<0,
z'=1-ln[1/(√x)^(√x)]-1/√x>0,x>1时,z单调递增,只要x->1时,z≥0即可;
x->1,z->1-m≥0,m≤1.
结合起来,m=1;
求解高三函数题
解:f’(x)=a-b/x^2
由题意得:f‘(1)=3,
则a-b=3,b=a-3
设F(x)=f(x)-3lnx=ax+(a-3)/x+3-2a-3lnx,(x属于[1,正无穷))
则F(x)>=0在[1,正无穷)上恒成立
F‘(x)=f'(x)-3/x=a-(a-3)/x^2-3/x
令F’(x)=0,解得:x=1.x=(3-a)/a
若(3-a)/a<=1,即a>=3/2,
Fmin=F(1)=a+a-3+3-2a>=0,恒成立。
若(3-a)/a>1,即0<a<3/2,
Fmin=F(3-a)/a))=3-a-a+3-2a-3ln(3-a)/a>=0
6-4a-3ln(3-a)/a>=0
这个方程不太好解,个人觉得f(x)应该为ax+b/x+3+2a,要不算到这步,真不好解~~~如果是+2a的话,解得a>=3/(1+e^2),最后a范围[3/(1+e^2),正无穷)
如果题没错,那我解不出来了~~~~~
高三试题,要详细过程,急急急: 已知函数f(x)=ax+lnx(a∈R), ①若a=2,求曲线y=f(x)在x...
先考查 f(x)=k的解的情况。
结果是:
k<0时,无解(0个解);
k=0时,三个解;
0<k<2时,六个解;
k=2时,四个解;
k>2时,二个解。
要满足条件,则 方程 at^2+bt+c=0得有两个不同的解t1和t2,
且f(x)=t1和f(x)=t2的解:1)各有四个不同的解;2)一个方程有六个解,另一个方程有两个解。
由于f(x)=t1和f(x)=t2都有四个解时,则t1=t2=2,所以八个解两两相等,不满足。
因此,要得到八个不同的解,则 at^2+bt+c=0有两个不同的解t1和t2,
且0<t1<2,t2>2。
所以,由二次函数的性质,得(设g(t)=at^2+bt+c)
1)a>0,则 g(0)>0,且g(2)<0,解得 a>0且c>0且4a+2b+c<0;
或2)a<0,则 g(0)<0,g(2)>0,解得 a<0且c<0且4a+2b+c>0。
将以上两个条件合并,简化为: c≠0 且 a(4a+2b+c)<0,这就是所要求的充要条件。
(或者也可简化为:ac>0且4a+2b+c≠0; 或者:a≠0,c(4a+2b+c)<0。)
(那个答案是错误的,如 -[f(x)]^2+4f(x)-3=0有八个不同的解
x1=-2.10380,x2=-1.87939,x3=-1.53209,x4=-0.34730,
x5=-x4,x6=-x3,x7=-x2,x8=-x1)。
2道高考题外加1道函数题
a=2
f(x)=2x+lnx
f'(x)=x+1/x
x=1,f'(1)=2,f(1)=2
切线方程
y-2=2(x-1)
2x-y=0
f'(x)=a+1/x
若a≥0则
f'(x)=a+1/x>0
x>1/a时函数单增
若a<0则
f'(x)=a+1/x>0
无解
故a>0,x>1/a时函数单增
或a=0,x>0时函数单增
第一题
解:a平方+2ab+2ac+4bc=12
而:
2bc<=b平方+c平方
所以原式可化简为
a平方+2ab+2ac+2bc+2bc=12
a平方+2ab+2ac+2bc+b平方+c平方>=12
(a+b+c)平方>=12
a b c>0
a+b+c>=2根号3
第二题
解:
第一种情况:判别式<=0,=>a^2-4<=0,=>-2<=a<=2
第二种情况:判别式>=0,-a/2<=0,f(0)>=0,
=>a>=2
第三种情况:判别式>=0,-a/2>=1/2,f(1/2)>=0,
=>-5/2<=a<=-2
所以a的最小值为-5/2
第三题解:设f(x)=ax+b,则
f[f(x)]=a(ax+b)+b=a?x+ab+b=4x-1
因此a?=4.........(1)
ab+b=-1..........(2)
由(1)得a=±2.代入(2)式得:
(±2+1)b=-1,∴a=2时,b=-1/3; a=-2时,b=1.
故f(x)=2x-1/3或f(x)=-2x+1.
设f(x)=ax+b
为什么f(f(x))=af(x)+b ?
答:因为将括号内的f(x)看作一个整体,相当于一个x,此时的x=f(x),不知道你明白没?不明白的话可以给我发信息









